Posted on

Multitask learning is Black-Boxable

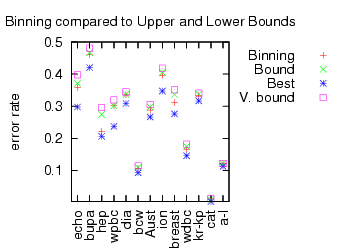
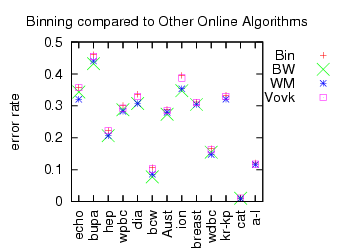
Multitask learning is the problem of jointly predicting multiple labels simultaneously with one system. A basic question is whether or not multitask learning can be decomposed into one (or more) single prediction problems. It seems the answer to this is “yes”, in a fairly straightforward manner.

The basic idea is that a controlled input feature is equivalent to an extra output. Suppose we have some process generating examples: (x,y1,y2) in S where y1 and y2 are labels for two different tasks. Then, we could reprocess the data to the form Sb(S) = {((x,i),yi): (x,y1,y2) in S, i in {1,2}} and then learn a classifier c:X x {1,2} -> Y. Note that (x,i) is the (composite) input. At testing time, given an input x, we can query c for the predicted values of y1 and y2 using (x,1) and (x,2).

A strong form of equivalence can be stated between these tasks. In particular, suppose we have a multitask learning algorithm ML which learns a multitask predictor m:X -> Y x Y. Then the following theorem can be proved:

For all ML for all S, there exists an inverse reduction Sm such that ML(S) = ML(Sm(Sb(S)).

In other words, no information is lost in the transformation Sb which means everything which was learnable previously remains learnable.

This may not be the final answer to the question because there may be some algorithm-dependent (mis)behavior associated with controlled feature i. It may also be the case that single task classification is computationally distinguishable from multitask classification. Certainly, computational concerns are one of the reasons specialized multitask classification algorithms exist.

Posted on

Online learning or online preservation of learning?

In the online learning with experts setting, you observe a set of predictions, make a decision, and then observe the truth. This process repeats indefinitely. In this setting, it is possible to prove theorems of the sort:

master algorithm error count < = k* best predictor error count + c*log(number of predictors)

Is this a statement about learning or about preservation of learning? We did some experiments to analyze the new Binning algorithm which works in this setting. For several UCI datasets, we reprocessed them so that features could be used as predictors and then applied several master algorithms. The first graph confirms that Binning is indeed a better algorithm according to the tightness of the upper bound.


Here, “Best” is the performance of the best expert. “V. Bound” is the bound for Vovk‘s algorithm (the previous best). “Bound” is the bound for the Binning algorithm. “Binning” is the performance of the Binning algorithm. The Binning algorithm clearly has a tighter bound, and the performance bound is clearly a sharp constraint on the algorithm performance.

Instead of examining bounds, we can simply look at performance.


“Bin” is the performance of Binning (identical to the previous graph). BW is Binomial weighting, which is (roughly) the deterministic version of Binning. WM is Weighted Majority. Both BW and WM are deterministic algorithms which implies their performance bounds are perhaps a factor of 2 worse than Binning or Vovk’s algorithm.

In contrast, the actual performance (rather than performance bound) of the deterministic algorithms is sometimes even better than the best expert (negative regret?!). A consistent negative correlation between “online bound tightness” and “learning performance” is observed.

The question is “What’s happening here?”

  1. One reply is that we are testing in the wrong setting. These algorithms are designed to work in highly adversarial environments for which a UCI dataset does not qualify. This isn’t a convincing answer to me because many (or perhaps most) situations are not that adversarial.
  2. Another answer is “you used the wrong experts”. This is not convincing because many other learning algorithm do as well or better with the given features/experts.
  3. Another possibility is “you can start out running Binning, and when it pulls ahead of it’s bound run any learning algorithm. If the learning algorithm does badly, you can switch back to Binning and preserve the guarantee.” So, Binning is effectively a safety net.

My best current understanding is that “online learning with experts” is really “online preservation of learning”: the goal of the algorithm is to preserve whatever predictive ability the individual predictors have. This understanding fits the form of the theory statement well.

Preservation is desirable in some situations. For example, charity events sometimes work according to the following form:

  1. All participants exchange dollars for bogobucks.
  2. The participants gamble with bogobucks.
  3. The winner at the end gets some prize.

An online preservation algorithm has the property that if you acquire enough bogobucks in comparison to the number of participants, you can guarantee winning the prize. These kinds of ‘winner take all’ scenarios come up elsewhere.

Posted on

Use of Notation

For most people, a mathematical notation is like a language: you learn it and stick with it. For people doing mathematical research, however, this is not enough: they must design new notations for new problems. The design of good notation is both hard and worthwhile since a bad initial notation can retard a line of research greatly.

Before we had mathematical notation, equations were all written out in language. Since words have multiple meanings and variable precedences, long equations written out in language can be extraordinarily difficult and sometimes fundamentally ambiguous. A good representative example of this is the legalese in the tax code. Since we want greater precision and clarity, we adopt mathematical notation.

One fundamental thing to understand about mathematical notation, is that humans as logic verifiers, are barely capable. This is the fundamental reason why one notation can be much better than another. This observation is easier to miss than you might expect because, for a problem that you are working on, you have already expended the effort to reach an understanding.

I don’t know of any systematic method for designing notation, but there are a set of heuristics learned over time which may be more widely helpful.

  1. Notation should be minimized. If there are two ways to express things, then choose the (objectively, by symbol count) simpler one. If notation is only used once, it should be removable (this often arises in presentations).
  2. Notation divergence should be minimized. If the people working on some problem have a standard notation, then sticking with it is easier. For example, in machine learning x is almost always a set of features from which predictions are made.
  3. A reasonable mechanism for notation design is to first name and define the quantities you are working with (for example, reward r and time t), and then make derived quantities by combination (for example rt is reward at time t).
  4. Variables should be alliterated. Time is t, reward is r, cost is c, hypothesis is h.
  5. Name collisions (or near collisions) should be avoided. E and p are terrible variable names in some contexts.
  6. Sub-sub-scripts should be avoided. It is often possible to change a sub-sub-script into a sub-script by redefinition.
  7. Superscripts are dangerous because of overloading with exponentiation.
  8. Inessential dependences should be suppressed in the definition. (For example, in reinforcement learning the MDP M you are working with is often suppressable because it never changes.)
  9. A dependence must be either uniformly suppressed or uniformly explicit.
  10. Short theorem statements are very nice. There seem to be two styles of theorem statements: long including all definitions and short with definitions made before the statement. As computer scientists, we have to prefer “short” because long is nonmodular. As humans, it’s easier to read.
  11. It is very easy to forget the quantification of a variable (“for all” or “there exists”) when you are working on a theorem, and it is essential for readers that you specify it explicitly.
  12. Avoid strange alphabets. It is hard for people to think with unfamiliar symbols. english lowercase > english upper case > greek lower case > greek upper case > hebrew > other strange things.
  13. The definitions section of a paper often should not contain all the definitions in a paper. Instead, it should cover the universally used definitions. Others can be introduced just before they are used.

These heuristics often come into conflict, which can be hard to resolve. When trying to resolve the conflict, it’s important to understand that it’s easy to fail to imagine what a notation would be like. Trying out different notations and comparing is reasonable.

Are there other useful heuristics for notation design? (Or disagreements with the above heuristics?)

Posted on

“Structural” Learning

Fernando Pereira pointed out Ando and Zhang‘s paper on “structural” learning. Structural learning is multitask learning on subproblems created from unlabeled data.

The basic idea is to take a look at the unlabeled data and create many supervised problems. On text data, which they test on, these subproblems might be of the form “Given surrounding words predict the middle word”. The hope here is that successfully predicting on these subproblems is relevant to the prediction of your core problem.

In the long run, the precise mechanism used (essentially, linear predictors with parameters tied by a common matrix) and the precise problems formed may not be critical. What seems critical is that the hope is realized: the technique provides a significant edge in practice.

Some basic questions about this approach are:

  1. Are there effective automated mechanisms for creating the subproblems?
  2. Is it necessary to use a shared representation?
Posted on

Why do people count for learning?

This post is about a confusion of mine with respect to many commonly used machine learning algorithms.

A simple example where this comes up is Bayes net prediction. A Bayes net where a directed acyclic graph over a set of nodes where each node is associated with a variable and the edges indicate dependence. The joint probability distribution over the variables is given by a set of conditional probabilities. For example, a very simple Bayes net might express:
P(A,B,C) = P(A | B,C)P(B)P(C)

What I don’t understand is the mechanism commonly used to estimate P(A | B, C). If we let N(A,B,C) be the number of instances of A,B,C then people sometimes form an estimate according to:

P'(A | B,C) = N(A,B,C) / N /[N(B)/N * N(C)/N] = N(A,B,C) N /[N(B) N(C)]

… in other words, people just estimate P'(A | B,C) according to observed relative frequencies. This is a reasonable technique when you have a large number of samples compared to the size space A x B x C, but it (naturally) falls apart when this is not the case as typically happens with “big” learning problems such as machine translation, vision, etc…

To compensate, people often try to pick some prior (such as Dirichlet prior with one “virtual count” per joint parameter setting) to provide a reasonable default value for the count. Naturally, in the “big learning” situations where this applies, the precise choice of prior can greatly effect the system performance leading to finicky tuning of various sorts. It’s also fairly common to fit some parametric model (such as a Gaussian) in an attempt to predict A given B and C.

Stepping back a bit, we can think of the estimation of P(A | B, C) as a simple self-contained prediction (sub)problem. Why don’t we use existing technology for doing this prediction? Viewed as a learning algorithm “counting with a Dirichlet prior” is exactly memorizing the training set and then predicting according to either (precisely) matching training set elements or using a default. It’s hard to imagine a more primitive learning algorithm.

There seems to be little downside to trying this approach. In low count situations, a general purpose prediction algorithm has a reasonable hope of performing well. In a high count situation, any reasonable general purpose algorithm converges to the same estimate as above. In either case something reasonable happens.

Using a general purpose probabilistic prediction algorithm isn’t a new idea, (for example, see page 57), but it appears greatly underutilized. This is a very small modification of existing systems with a real hope of dealing with low counts in {speech recognition, machine translation, vision}. It seems that using a general purpose probabilistic prediction algorithm should be the default rather than the exception.