Online learning or online preservation of learning?

In the online learning with experts setting, you observe a set of predictions, make a decision, and then observe the truth. This process repeats indefinitely. In this setting, it is possible to prove theorems of the sort:

master algorithm error count < = k* best predictor error count + c*log(number of predictors)

Is this a statement about learning or about preservation of learning? We did some experiments to analyze the new Binning algorithm which works in this setting. For several UCI datasets, we reprocessed them so that features could be used as predictors and then applied several master algorithms. The first graph confirms that Binning is indeed a better algorithm according to the tightness of the upper bound.

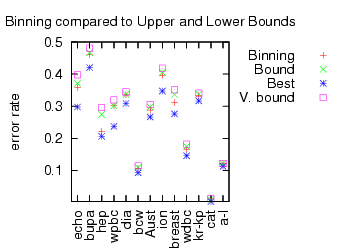
Here, “Best” is the performance of the best expert. “V. Bound” is the bound for Vovk‘s algorithm (the previous best). “Bound” is the bound for the Binning algorithm. “Binning” is the performance of the Binning algorithm. The Binning algorithm clearly has a tighter bound, and the performance bound is clearly a sharp constraint on the algorithm performance.

Instead of examining bounds, we can simply look at performance.

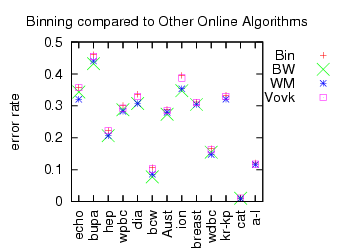
“Bin” is the performance of Binning (identical to the previous graph). BW is Binomial weighting, which is (roughly) the deterministic version of Binning. WM is Weighted Majority. Both BW and WM are deterministic algorithms which implies their performance bounds are perhaps a factor of 2 worse than Binning or Vovk’s algorithm.

In contrast, the actual performance (rather than performance bound) of the deterministic algorithms is sometimes even better than the best expert (negative regret?!). A consistent negative correlation between “online bound tightness” and “learning performance” is observed.

The question is “What’s happening here?”

1. One reply is that we are testing in the wrong setting. These algorithms are designed to work in highly adversarial environments for which a UCI dataset does not qualify. This isn’t a convincing answer to me because many (or perhaps most) situations are not that adversarial.
2. Another answer is “you used the wrong experts”. This is not convincing because many other learning algorithm do as well or better with the given features/experts.
3. Another possibility is “you can start out running Binning, and when it pulls ahead of it’s bound run any learning algorithm. If the learning algorithm does badly, you can switch back to Binning and preserve the guarantee.” So, Binning is effectively a safety net.

My best current understanding is that “online learning with experts” is really “online preservation of learning”: the goal of the algorithm is to preserve whatever predictive ability the individual predictors have. This understanding fits the form of the theory statement well.

Preservation is desirable in some situations. For example, charity events sometimes work according to the following form:

1. All participants exchange dollars for bogobucks.
2. The participants gamble with bogobucks.
3. The winner at the end gets some prize.

An online preservation algorithm has the property that if you acquire enough bogobucks in comparison to the number of participants, you can guarantee winning the prize. These kinds of ‘winner take all’ scenarios come up elsewhere.