Maverick Woo and the Aladdin group at CMU have started a CS theory-related blog here.
Dynamic Programming Generalizations and Their Use
David Mcallester gave a talk about this paper (with Pedro Felzenszwalb). I’ll try to give a high level summary of why it’s interesting.
Dynamic programming is most familiar as instantiated by Viterbi decoding in a hidden markov model. It is a general paradigm for problem solving where subproblems are solved and used to solve larger problems. In the Viterbi decoding example, the subproblem is “What is the most probable path ending at each state at timestep t?”, and the larger problem is the same except at timestep t+1. There are a few optimizations you can do here:
- Dynamic Programming -> queued Dynamic Programming. Keep track of the “cost so far” (or “most probable path”) and (carefully) only look at extensions to paths likely to yield the shortest path. “Carefully” here is defined by Dijkstra’s shortest path algorithm.
- queued Dynamic programming -> A*Add a lower bound on the cost to complete a path (or an upper bound on the probability of a completion) for the priority queue of Dijkstra’s shortest path. This can yield computational speedups varying between negligible and outstanding.
- A* -> Hierarchical A* The efficiency of A* search is dependent on the tightness of it’s lower bound, which brings up the question: “Where do you get the lower bound?” One appealing answer is from A* applied to a simplified problem equivalent to the original problem, but with states aliased (many states in original problem = 1 state in new problem). This technique can be applied recursively until the problem is trivial.
Each of these steps has been noted previously (although perhaps not in the generality of this paper). What seems new and interesting is that the entire hierarchy of A* searches can be done simultaneously on one priority queue.
The resulting algorithm can use low level information to optimize high level search as well as high level information to optimize low level search in a holistic process. It’s not clear yet how far this approach can be pushed, but this quality is quite appealing. Naturally, there are many plausible learning-related applications.
Which Assumptions are Reasonable?
One of the most confusing things about understanding learning theory is the vast array of differing assumptions. Some critical thought about which of these assumptions are reasonable for real-world problems may be useful.
Before we even start thinking about assumptions, it’s important to realize that the word has multiple meanings. The meaning used here is “assumption = axiom” (i.e. something you can not verify).
| Assumption | Reasonable? | Which analysis? | Example/notes |
| Independent and Identically Distributed Data | Sometimes | PAC,ERM,Prediction bounds,statistics | The KDD cup 2004 physics dataset is plausibly IID data. There are a number of situations which are “almost IID” in the sense that IID analysis results in correct intuitions. Unreasonable in adversarial situations (stock market, war, etc…) |
| Independently Distributed Data | More than IID, but still only sometimes | online->batch conversion | Losing “identical” can be helpful in situations where you have a cyclic process generating data. |
| Finite exchangeability (FEX) | Sometimes reasonable | as for IID | There are a good number of situations where there is a population we wish to classify, pay someone to classify a random subset, and then try to learn. |
| Input space uniform on a sphere | No. | PAC, active learning | I’ve never observed this in practice. |
| Functional form: “or” of variables, decision list, “and” of variables | Sometimes reasonable | PAC analysis | There are often at least OK functions of this form that make good predictions |
| No Noise | Rarely reasonable | PAC, ERM | Most learning problems appear to be of the form where the correct prediction given the inputs is fundamentally ambiguous. |
| Functional form: Monotonic on variables | Often | PAC-style | Many natural problems seem to have behavior monotonic in their input variables. |
| Functional form: xor | Occasionally | PAC | I was suprised to observe this. |
| Fast Mixing | Sometimes | RL | Interactive processes often fail to mix, ever, because entropy always increases. |
| Known optimal state distribution | Sometimes | RL | Sometimes humans know what is going on, and sometimes not. |
| Small approximation error everywhere | Rarely | RL | Approximate policy iteration is known for sometimes behaving oddly. |
If anyone particularly agrees or disagrees with the reasonableness of these assumptions, I’m quite interested.
Families of Learning Theory Statements
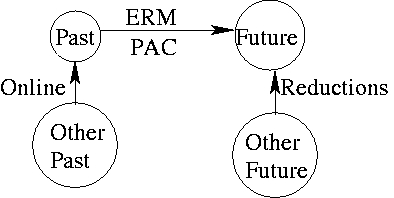
The diagram above shows a very broad viewpoint of learning theory.
| arrow | Typical statement | Examples |
| Past->Past | Some prediction algorithm A does almost as well as any of a set of algorithms. | Weighted Majority |
| Past->Future | Assuming independent samples, past performance predicts future performance. | PAC analysis, ERM analysis |
| Future->Future | Future prediction performance on subproblems implies future prediction performance using algorithm A. | ECOC, Probing |
A basic question is: Are there other varieties of statements of this type? Avrim noted that there are also “arrows between arrows”: generic methods for transforming between Past->Past statements and Past->Future statements. Are there others?
Is the Goal Understanding or Prediction?
Steve Smale and I have a debate about goals of learning theory.
Steve likes theorems with a dependence on unobservable quantities. For example, if D is a distribution over a space X x [0,1], you can state a theorem about the error rate dependent on the variance, E(x,y)~D (y-Ey’~D|x[y’])2.
I dislike this, because I want to use the theorems to produce code solving learning problems. Since I don’t know (and can’t measure) the variance, a theorem depending on the variance does not help me—I would not know what variance to plug into the learning algorithm.
Recast more broadly, this is a debate between “declarative” and “operative” mathematics. A strong example of “declarative” mathematics is “a new kind of science”. Roughly speaking, the goal of this kind of approach seems to be finding a way to explain the observations we make. Examples include “some things are unpredictable”, “a phase transition exists”, etc…
“Operative” mathematics helps you make predictions about the world. A strong example of operative mathematics is Newtonian mechanics in physics: it’s a great tool to help you predict what is going to happen in the world.
In addition to the “I want to do things” motivation for operative mathematics, I find it less arbitrary. In particular, two reasonable people can each be convinced they understand a topic in ways so different that they do not understand the viewpoint. If these understandings are operative, the rest of us on the sidelines can better appreciate which understanding is “best”.